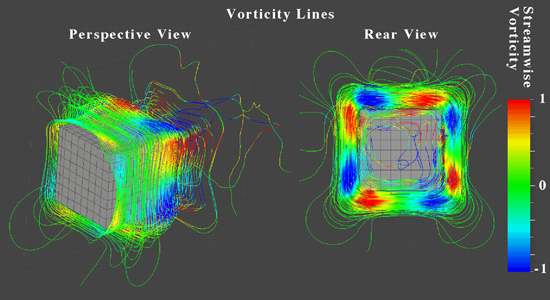
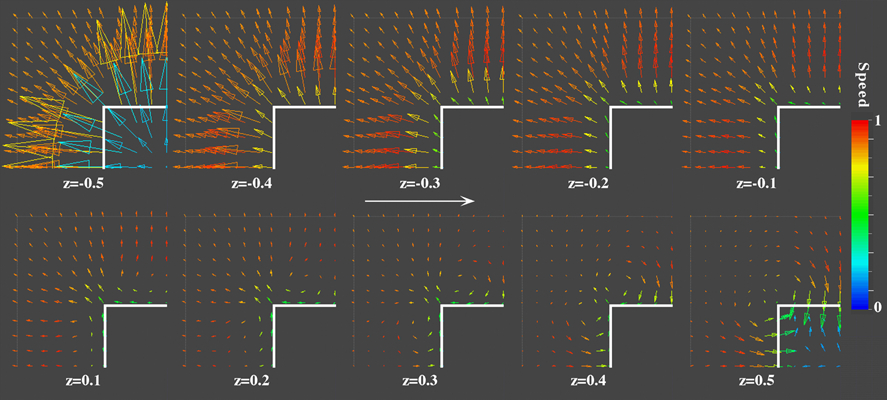
Motivation

Simulation of flow over cubes is relevant to a large number of industrial applications such as: convective cooling of microprocessor chips or buildings, drag and noise reduction in cars and trucks, or control of wind-induced vibrations in highrises. The cube geometry is very simple, yet the flow around it manifests interesting 3-D structures that are prominent in more complex configurations.

A little about the method

The following are some grid-free simulation results at Reynolds number 100 (based on the cube side and the free-stream velocity), flowing from left to right. Refer to [6] for details and for the case of Reynolds number 1,000.

The above animation is a display of the initial stages of the flow development in the plane of symmetry of the cube. The solid circles depict the location of the computational elements, and the line segments originating from their centers represent the local velocity. Blue=high velocity, and red=low velocity. Note that these are not post-processed passive elements, but the actual computational elements which are generated at the boundary of the cube (to satisfy the no-slip boundary condition), and which evolve in the fluid in the Lagrangian frame of reference.

The computational elements are vorticity weighted and hence are called vortex elements. Note that these vortex elements are concentrated within the boundary layer of the cube faces and the wake behind the cube, where vorticity is significant. Outside this region, where the flow is essentially potential, no elements can be seen. More importantly, the element locations are not assigned a priori by the user, but determined dynamically by the flow itself.

Some physics

The wake behind the cube, while symmetric during the early stages of its formation, is highly unsteady and asymmetric due to the introduction of random, noise-level disturbances to the flow field. If the flow is in the stable regime; e.g., laminar duct flow, the perturbations do not grow. However, if the flow is inherently unstable the random perturbations give rise to unsteady dynamics. The fundamental non-dimensional frequency (Strouhal number) of oscillation of the near-field wake is found to be S = 0.143 for the cube,which is close to the shedding frequency of the flow over a square rod (S = 0.148-0.153) at the same Reynolds number.

Note that although the instantaneous flow over the cube is non-symmetric, its time-averaged topology is symmetric.

The above figure depicts a set of stationary state vorticity lines around the cube. It shows the existence of four pairs of oppositely-signed very weak streamwise vortices at the four upstream corners of the cube. This is caused by the tendency of the flow at the upstream face, which is directed radially outward from the stagnation point, to re-orient itself in the direction of the freestream flow. Additionally, starting from midway between the upstream and downstream faces of the cube, a pair of oppositely signed streamwise vortices (with growing intensity toward the downstream face) are generated on each face of the cube and extend out into the wake - prominently forming what appears as four pairs of horseshoe-like vortices around the cube. The process leading to the development of these streamwise vortices can be explained by a simple ring model. The vorticity lines around the cube (closer to the upstream face) form square-shaped rings. The high curvatures at the four corners push them forward at a faster rate than the remainder of the ring, causing the initiation and subsequent growth of streamwise vortices.