Motivation

A well-known disadvantage of traditional (non-adaptive) CFD algorithms is that they suffer from high numerically induced diffusion. The excessive damping caused by numerical diffusion inhibits the growth of inviscid instabilities observed in typical turbulent flow scenarios, and it leads to the premature dissipation of coherent vortical structures of interest to industrial applications, such as the wake behind airfoils or bluff bodies, or the vortical flow in IC engines. In other words, numerical diffusion tends to "laminarize" otherwise turbulent flow simulations.

In contrast, thanks to the Lagrangian nature of the computation, our simulations are virtually free of numerical diffusion. This allows us to model and capture complex turbulent vortical structures with minimal computational effort, as evidenced with the example on this page.

LES of A "Fat" Vortex Ring

This is a "simple" but very powerful demonstration of the robustness of any method that would be used to predict and study turbulent flow. Yet, the vortex ring problem is a prototype model, the understanding of the dynamics of which is relevant to many industrial and military applications. One example is the study of vortex ring formation and development due to the jet exhaust of aircraft engines with different cross-sectional configurations for the exhaust.

It is quite well-known that when a vortex ring is perturbed sinusoidally in the radial direction around the azimuth of the ring, the perturbations will re-orient themselves along the streamwise direction and, given the proper wave-number, will grow inviscidly in that direction. If the CFD algorithm used is too diffusive, streamwise vorticies never develop and the vortex ring laminarizes.

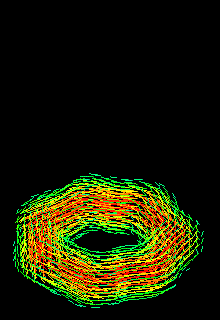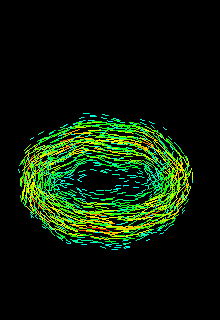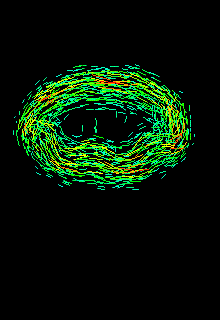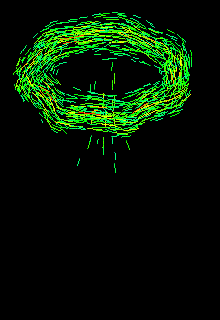
In this example, we demonstrate the robustness of our method using the LES of a vortex ring with vortex core to ring radius ratio of 0.45 - thus the term "fat" ring. The vortex core distribution is initially a cubic Gaussian and the ring is perturbed sinusoidally around its azimuth with the most unstable wave-number (=7) and 5% perturbation amplitude. A standard Smagorinsky LES model is used in this case, and the ring propagates by its self-induced velocity in free space at infinite Reynolds number.

The animation at the top of the page depicts the perspective view of the evolution of selected vortex particles (the actual computational elements), color coded by the vorticity magnitude (red being the highest and blue being the lowest values). The "sticks" depict the direction of the vorticity vectors. The animation clearly demonstrates the ability of our method to capture the re-orientation and growth of the perturbations in the streamwise direction. It also captures the development of weak streamwise hairpin vortices (toward the ring center). This is an indication of the absence of significant numerical diffusion despite the fact that this is a low-resolution simulation, initially using fewer than 4300 computational points.

Click on the animation to display the side-view of the evolution of all vortex elements (and thus the vorticity field) in time. The solution-based adaptivity of our method is clearly visible: the elements automatically cluster where there is significant amount of vorticity and thus reproduce the familiar mushroom-shaped flow topology.

Once again, note the development of streamwise vortices within the ring core (focus on the orange/red vortex filaments), as well as the hairpin vortices in the weak wake behind the ring as it propels forward. These are experimentally observed features of the flow that cannot, in general, be captured by traditional CFD methods without the implementation of complex algorithms.