A Regularized Galerkin Boundary Element Method for 3D Potential Flow
Potenial Flow Normal To A
Parachute Model - Surface Mesh & Potential Jump Distributions
Motivation
The Lagrangian Vortex-Boundary Element simulation of flow about zero thickness membranes involves the prediction of a corresponding potential flow (via the derivative boundary integral equation for the Neumann problem describing the potential jump distribution on the surface).
This could be achieved by the commonly used Panel Method (PM), which assumes piecewise constant variation of the potential jump across the boundary elements/panels. Unfortunately, the velocity evaluations by the Panel Method are severely spiked and of O(1) accuracy for points that are proximal to the membrane surface - thus, adversely affecting the stability and the overall accuracy of the Vortex-Boundary Element simulations.
A Higher Order
Alternative
To this end, we have formulated a fully Regularized Galerkin Boundary Element Method (RGBEM) for high order prediction of 3D potential flow about zero thickness membranes [16], [17]. Two significant attributes of RGBEM are:
- C0 Continuity - Unlike classical BEM, where the continuity of the potential jump derivatives at the collocation points is a requisite, the Galerkin formulation requires the continuity of only the potential jump - thus simplifying the implementation of higher order approximants substantially.
- Regular Integrals - The regularization process in RGBEM has reduced the integrand singularity of the boundary integral equation by two orders, requiring a double surface integration that involves only the Green function for the potential!
For this project, we have implemented our RGBEM for linear variation of the potential jump across plane triangular elements.
Results
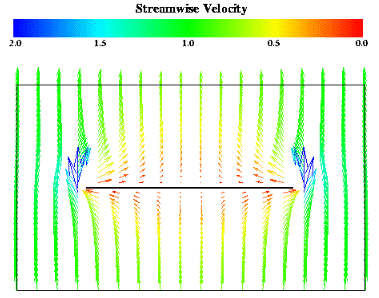
The robustness of RGBEM relative to PM was tested using the example of potential flow normal to a flat square plate (of unit sides). The following view of the velocity vector field at the plane of symmetry depicts the orientation of the plate and the direction of the flow. The plate is on the x-y plane and is centered at (x=y=0.5,z=0). The flow is in the positive z direction.
Potential Flow Normal To A Flat Square
Plate - Plane of Symmetry
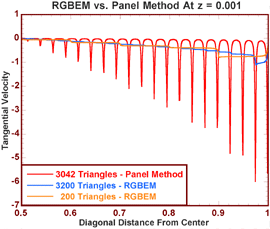
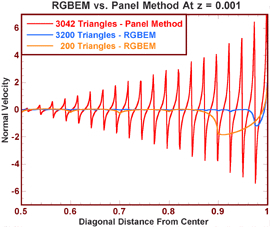
The following plots depict the tangential
and normal velocities at z=0.001, and along a
diagonal from the center to a corner of the plate - evaluated by PM and
linear RGBEM. 501 equidistant evaluation points were used for this
purpose. The diagonal distance is normalized by the diagonal length.
Note that the velocity profiles obtained by PM are severely spiked at points that correspond to the boundary element edges. This is because the potential jump is piecewise constant across the panels and its derivatives at the panel edges would necessarily yield spikes!
In contrast, the linear RGBEM leads to piecewise constant tangential velocities; i.e., no spikes as verified in the following plot. However, a log singularity exists in the normal component of the velocity; nevertheless, it is a significant improvement compared to the spikes due to the PM prediction.
In the following we note that the RGBEM profiles using only 200 triangular elements are better converged and smoother than the PM profiles using 3042 elements. Indeed, PM profiles using 12482 elements - a 62-fold increase in the number of elements - still display significant spikes!
Next, selected results from the RGBEM
simulation of potential flow around a hemispherical shell are
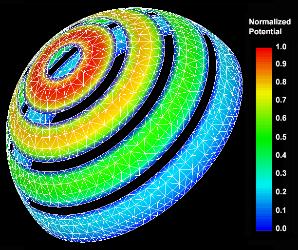
presented. The following figure depicts the mesh and potential jump
distributions on the surface of the shell, the axis of symmetry of
which is positioned along the freestream of unit speed. The potential
jump is normalized by its peak value of -1.945.
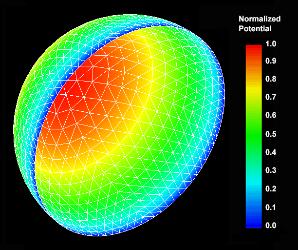
Potenial Flow Normal
To A Hemispherical Shell - Surface Mesh & Potential Jump Distributions
The following depicts the velocity vector
field proximal to the shell at its plane of symmetry. The velocity is
normalized by the maximum value in the displayed field. The shell
surface is color coded by the potential jump distribution.
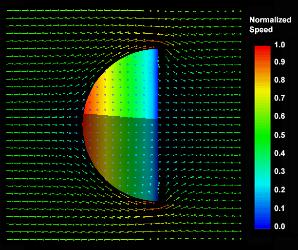
Potenial Flow Normal
To A Hemispherical Shell - Velocity Vector Field At Mid-Plane