A High Order Method for Grid-Free Diffusion In 3D Free Space
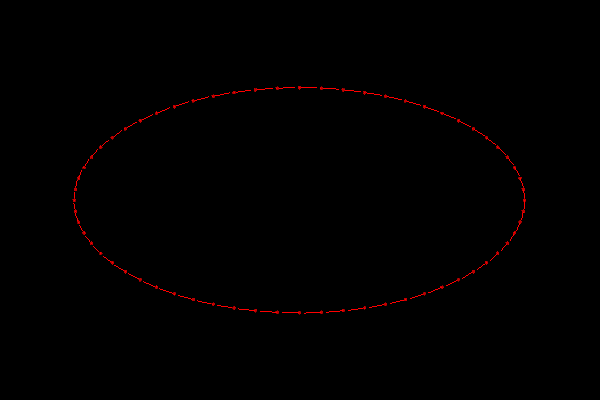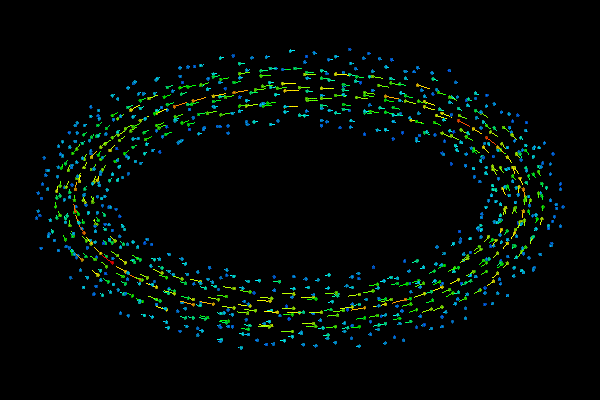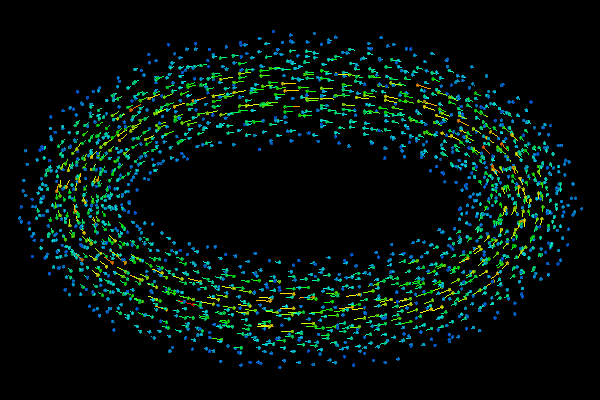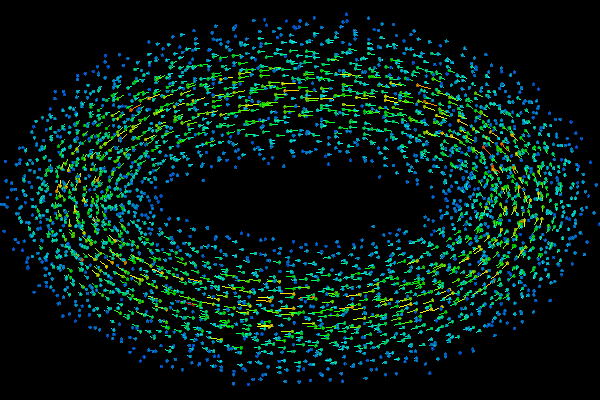
Grid-Free Diffusion
of A 3D Vortex Ring - Time Evolution of Vortex Particles
Motivation
The accurate and grid-free prediction of the diffusion of vorticity is an essential component of the Lagrangian Vortex-Boundary Element Method for viscous flow simulations.
Traditionally, diffusion has been emulated via the Random Walk Method, which is known for its low accuracy and convergence rate as well as the statistical noise it introduces to the computed flow field.
Alternatively, a number of deterministic methods for the accurate prediction of diffusion have been developed in recent years. Most of these methods are not truly grid-free as they require frequent remeshing onto a uniform background grid to improve long time solution accuracy. This diminshes the appeal of grid-free computing since remeshing is a fairly complex procedure near the boundaries, and it introduces some level of numerical diffusion into the computation. In addition, the positivity constraint precludes the formulation of arbitrarily high order schemes with most methods.
A High Order Truly Grid-Free
Alternative
A new deterministic scheme called the Vorticity Redistribution Method (VRM) [*] alleviates the above-mentioned difficulties altogether.
VRM simulates diffusion by redistributing fractions of the circulation of each vortex element to its neighboring elements, such that the conservation properties of the system and its positivity are preserved to arbitrarily high order. VRM may be considered to be an explicit grid-free finite-difference scheme, in which the fractions (the finite-difference coefficients) are the unknowns! The significant attributes of VRM are:
- Truly Grid-Free - Unlike other deterministic methods, VRM does not require frequent remeshing or a background grid to maintain long time accuracy, and it is free of numerical diffusion.
- Arbitrarily High Order with Positivity - VRM is capable of predicting diffusion at high accuracy and high rates of convergence, while maintaining positivity. Other methods can at best be second order accurate.
- Intelligent Particle Insertion Strategy - The VRM formulation mathematically detects when and where new vortex particles must be added to the computational domain to mimic the (physical) expansion of the vorticity field due to diffusion. Other methods use ad hoc user specified particle insertion strategies.
For this project, we have developed a (better than) third-order VRM for 3D diffusion of vorticity in free space [18],[19].
Results
2D Point Vortex
Singularity
The robustness of the high-order VRM is
demonstrated using the diffusion of a 2D point vortex singularity as
one test case. This is a vortex point with infinite
vorticity and zero support area, but
its circulation has value one.
We should emphasize here that no other deterministic method for diffusion can solve this problem, since they all discretize the vorticity field (which is initially singular) rather than circulation. In VRM, the point vortex is initialized using one particle with unit circulation. New particles are inserted in subsequent time-steps, as necessary, to emulate the expansion of the vorticity field due to diffusion. Note, since VRM is an explicit scheme, the inter-particle separation is nominally set in the order of the diffusion length scale for stability reasons. (Viscosity is one for this problem).
The following plots depict
(left) the vorticity profile
along (x, y = 0) at time T = 0.25, due to the diffusion of a point vortex
initially at (x = y = 0), as obtained by the Low-Order VRM [*]
(LO) using time-steps dt = 0.01 and dt = 0.001, and by the newly
developed High-Order VRM [18],[19]
(HO) using dt = 0.01; and
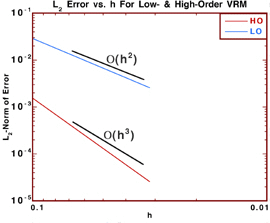
(right) the
LO and HO convergence rates, measured as the L2-norm of the error
versus the diffusion length scale.
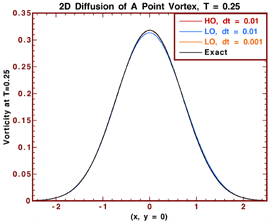
The figure on the left reveals that the
predictions by HO using dt = 0.01 and LO using dt
= 0.001 are indistinguishable from the exact
solution, whereas LO using dt = 0.01 displays some discrepancy.
Indeed, various test cases have demonstrated that HO
using an order
of magnitude larger time-step
than LO is more
accurate, and it requires about 3.5 times fewer particles and three
times less cumulative CPU time than does LO to solve this problem!
The figure on the right shows a second-order convergence rate (in inter-particle separation) for LO, and better than third-order (order 3.6) for HO. This is a significant achievement since all other grid-free methods can at best be second-order to maintain positivity.
2D Point Vortex
Pair
This example demonstrates how effortlessly
complex topologies are handled by VRM; e.g., the interface between
oppositely signed vorticity fields as they approach each other. Here, a
pair of vortex points with unit initial separation, and with infinite
vorticity and zero support area, and circulation
values ±one are diffused into each
other with unit viscosity.
The following animation depicts the time evolution of the scattered computational elements (vortex particles), which are color coded by their circulation values.

Grid-Free Diffusion of A 2D Vortex Pair
- Time Evolution of the Vortex Particles
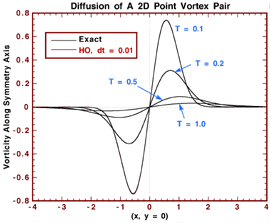
The following figure depicts the corresponding vorticity profile along (x, y
= 0) at various time levels, as obtained by the new High-Order VRM (HO)
using dt = 0.01. The predictions match the exact solution with
excellent accuracy. Note how well the symmetry of the vorticity field
as well as the slopes of the profiles near the axis of symmetry are
captured, despite the fact that the particles are not distributed with
any particular order and/or regularity.
3D Vortex Ring
The 3D high-order VRM is as accurate and
as simple to implement as the 2D case. Here we demonstrate this
capability by simulating the diffusion of a 3D infinitesimally thin
vortex ring with unit radius, circulation and viscosity.
The evolution of the vortex particles in time is animated in the figure at the top of this page. Again, note that the particles are scattered with no particular order. More importantly, no special care is necessary to accommodate the "gridding" of the ever shrinking inner hole in the "donut" as the vortex ring/torus expands. That is, the same strategy that is used to diffuse an isolated point vortex is used to diffuse the torus front as it merges with itself in the inner section of the donut.
The following figure depicts a cross-sectional cut and selected vortex tubes from the diffused vortex ring at time level T = 0.2, as predicted by HO using t = 0.01. The colors represent the vorticity magnitude normalized by the maximum in the field. Note how well the field symmetry is preserved.
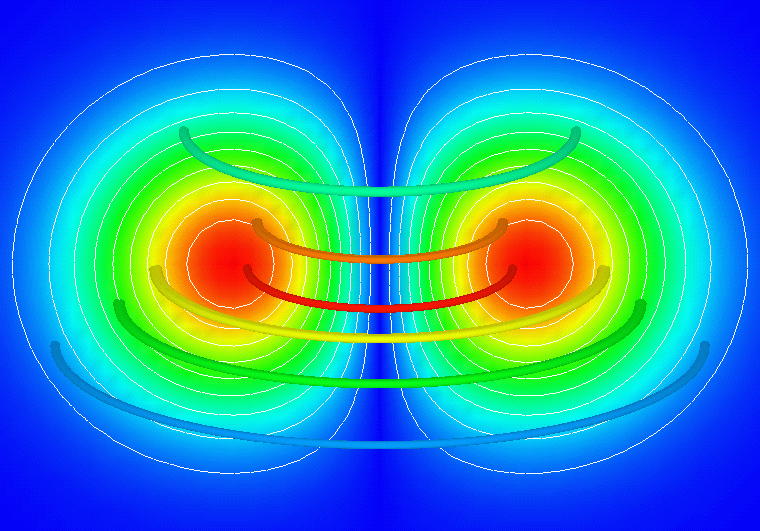
A Representative Cut of
the Vorticity Field At Time Level T = 0.2
* S. Shankar and L. van Dommelen, "A new Diffusion Procedure for Vortex Methods," Journal of Computational Physics, Vol. 127, pp. 88-109, 1996.